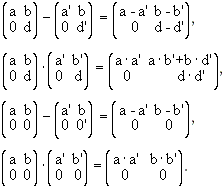Ideal In Abstract Algebra

For example the set of even integers is an ideal in the ring of integers.

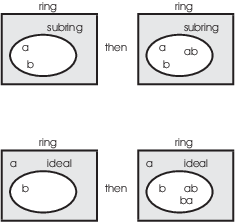
Ideal in abstract algebra. In ring theory a branch of abstract algebra an ideal is a special subset of a ring. Because 2 3 5 is not an element of either idealhence i u j is not an ideal of zfor this example is the smallest ideal containing and i hope this helps. Addition and subtraction of even numbers preserves evenness and multiplying an even number by any other integer results in another even number. A i is an additive subgroup of r b given r in r ain i then ra in i and ar in i.

A nonempty subset i of r is called an ideal only dealing with two sided as of this point of r if. And it satisfies. An ideal number is a nonempty set of numbers that satisfies those two properties even if we dont know what n is. Give an example of a ring a and ideals ij such that i u j is not an ideal.

We can pretend there is an n if we want but later we begin to think of the ideal numbers like n as being even better than just plain old numbers like n. Ideals generalize certain subsets of the integers such as the even numbers or the multiples of 3. Given an ideal it is possible to define a quotient ring. Ideals are commonly denoted using a gothic typeface.

These closure and absorption properties are the defining properties of an ideal. An ideal is prime if it satisfies. An ideal is maximal if it is proper ie. For any ideals a and b such that ab is a subset of i implies a is in i or b is in i.