Examples Of Fields Abstract Algebra
For simplicity the fields of prime characteristic that i use in this course will almost always be finite.

Examples of fields abstract algebra. Fields are a key structure in abstract algebra. Fields of prime characteristic and are fields since 2 3 and 61 are prime. The set fx of all polynomials with coefficients in a field f. Review and a look ahead.
Introduction to groups rings and fields ht and tt 2011 h. Any field f in particular the set q of rational numbers and the set r of real numbers. The set of integers z. On the other hand is not a field since 6 isnt prime because.
Grf is an algebra course and specically a course about algebraic structures. The set z n of integers modulo n. A set of integer numbers is a ring with respect to addition and multiplication. In mathematics a field is a set on which addition subtraction multiplication and division are defined and behave as the corresponding operations on rational and real numbers do.
This introduc tory section revisits ideas met in the early part of analysis i and in linear algebra i to set the scene and provide. The best known fields are the field of rational numbers the field of real. A field is thus a fundamental algebraic structure which is widely used in algebra number theory and many other areas of mathematics. Have an idea about abstract algebra particularly group theory in hisher undergraduate.
Today we give lots of examples of infinite fields including the rational numbers real numbers complex numbers and more. A fieldis a ring such thatfor any a that is not equal to 0 there is an element b thatis inverse to a with respect to multiplication. Isa commutative ring with identity. Commutative rings in general the examples to keep in mind are these.
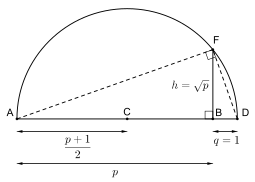
Show that a b3 a b q is a field a subfield of the field r but a b3 a b z is not a field. We also show you how to extend fields using polynomial equations and convergent sequences.
















































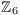












/confused-girl-in-front-of-a-blackboard-full-of-formulas--947690882-5af49088eb97de003d93de23.jpg)