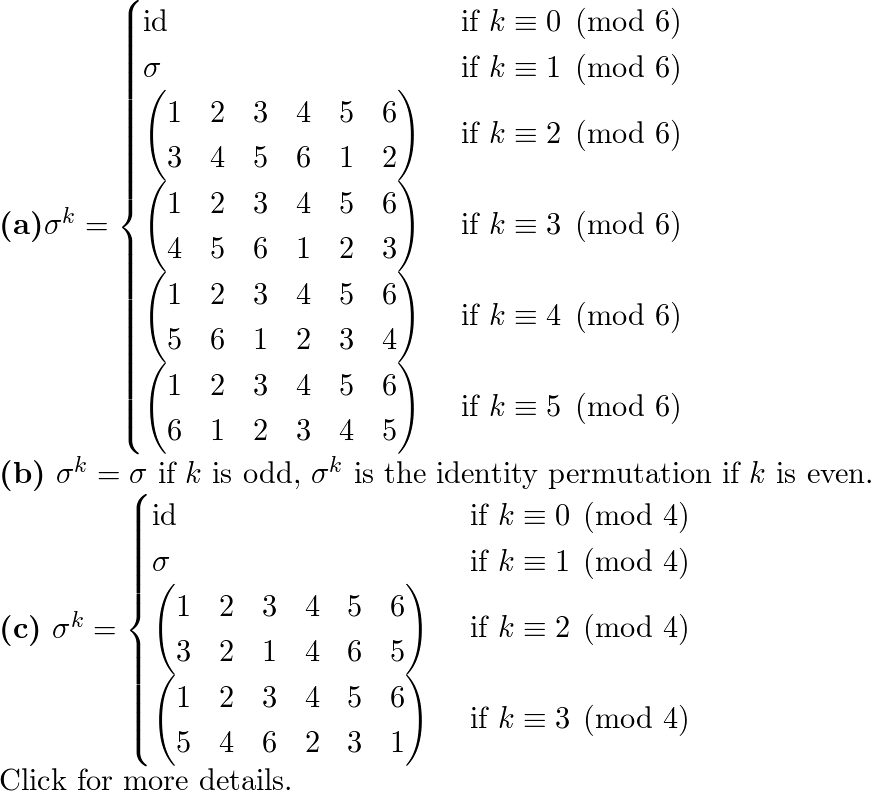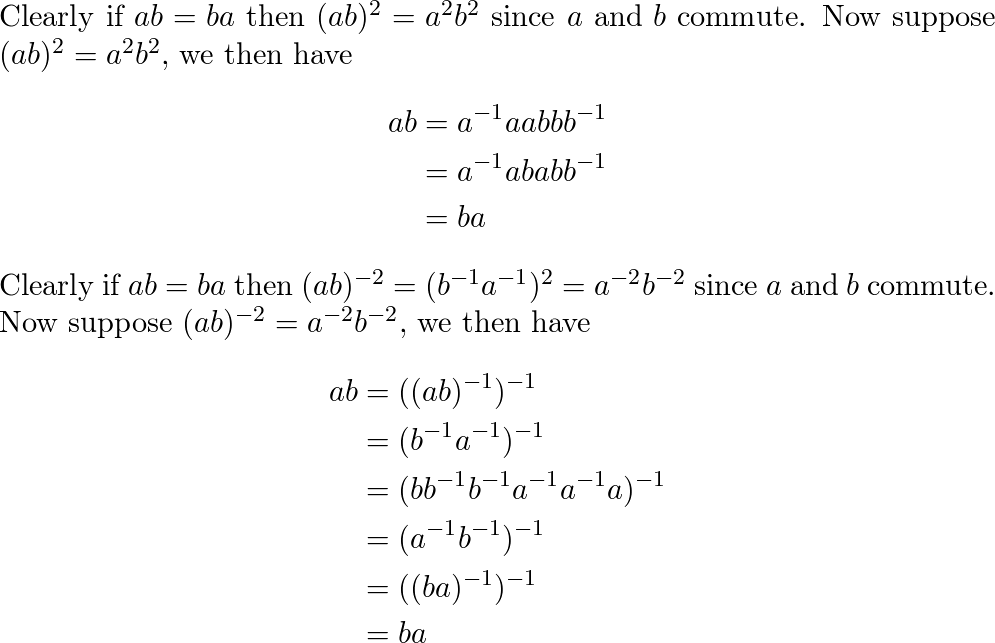Abstract Algebra Vs Linear Algebra

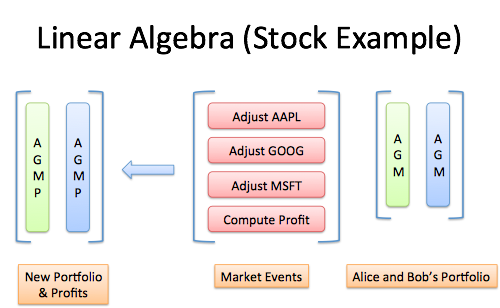
Linear algebra services numerous fields and while abstract algebra is certainly of great importance it can be argued successfully that linear algebra equips one with plenty of immediate tools for use in many areas.

Abstract algebra vs linear algebra. I took linear algebra my junior year in high school. The book addresses the conventional topics. Around the level of an intro course just knowing the basics of rings groups ideals the first isomorphism theorem. I use linear algebra quite a lot in applications but i do not have a very strong abstract algebra background ie.

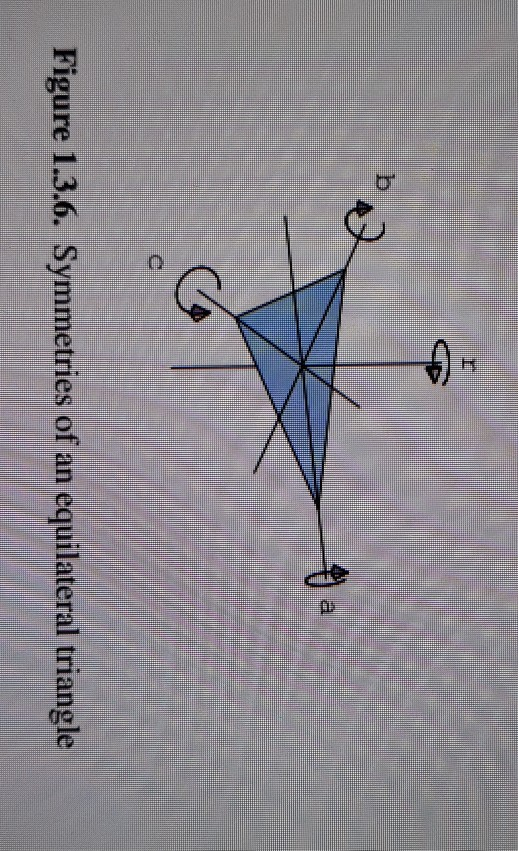
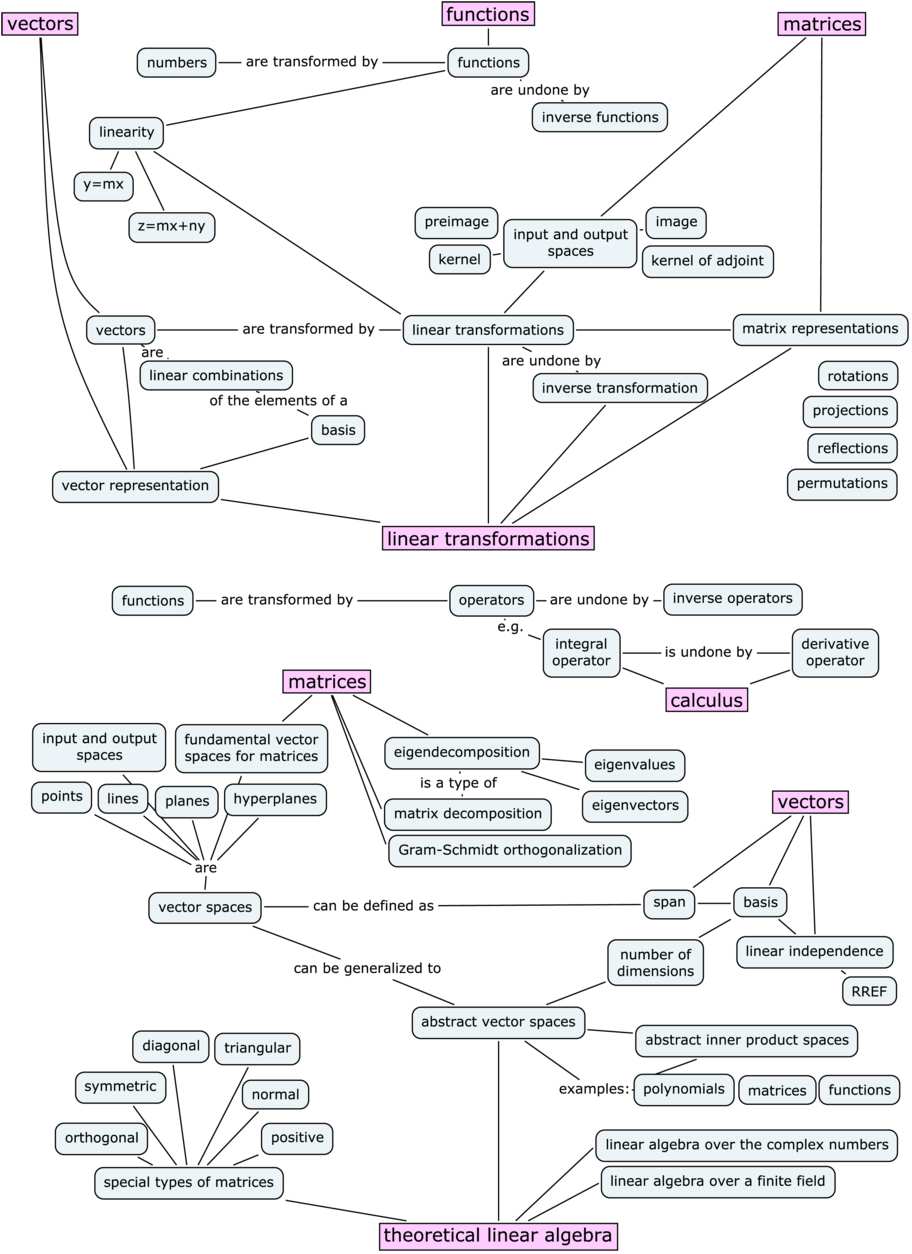
In algebra which is a broad division of mathematics abstract algebra occasionally called modern algebra is the study of algebraic structuresalgebraic structures include groups rings fields modules vector spaces lattices and algebrasthe term abstract algebra was coined in the early 20th century to distinguish this area of study from the other parts of algebra. You cant ignore abstract algebra though if you later learn linear algebra at advanced math such as algebraic topology homology co homology which uses mainly linearlisation aka linear maps you need to know the basic abstract algebra stuff eg. Linear algebra is part of abstract algebra in vector space group semi ring however it is more concrete with matrices hence less abstract and easier to learn. Abstract algebra deals with various abstract structures such as groups rings and fields.

A field is the nicest structure for the common people since in a field all of the arithmetic and algebra that you have learned since elementary school works. Linear algebra is the study of vector spaces and linear mappings between those spaces. The concepts are fairly abstract. Based on the short description of applied linear algebra i believe that the applied la.

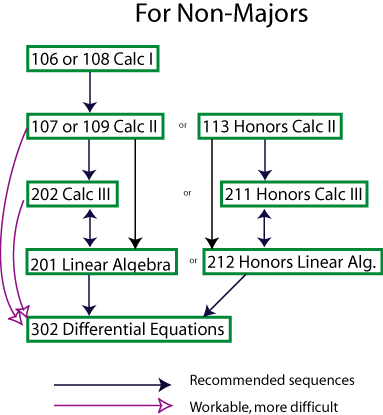
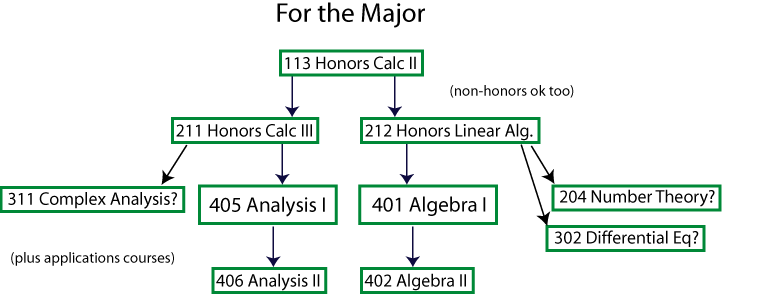
Linear equations matrices vector spaces linear transformations determinants eigenvalues and inner product spaces. Sets and mappings groups and subgroups homomorphisms and isomorphisms permutations rings and domains arithmetic properties of domains and fields.