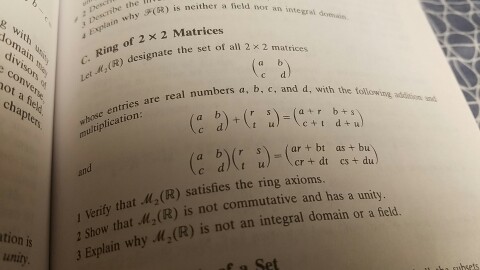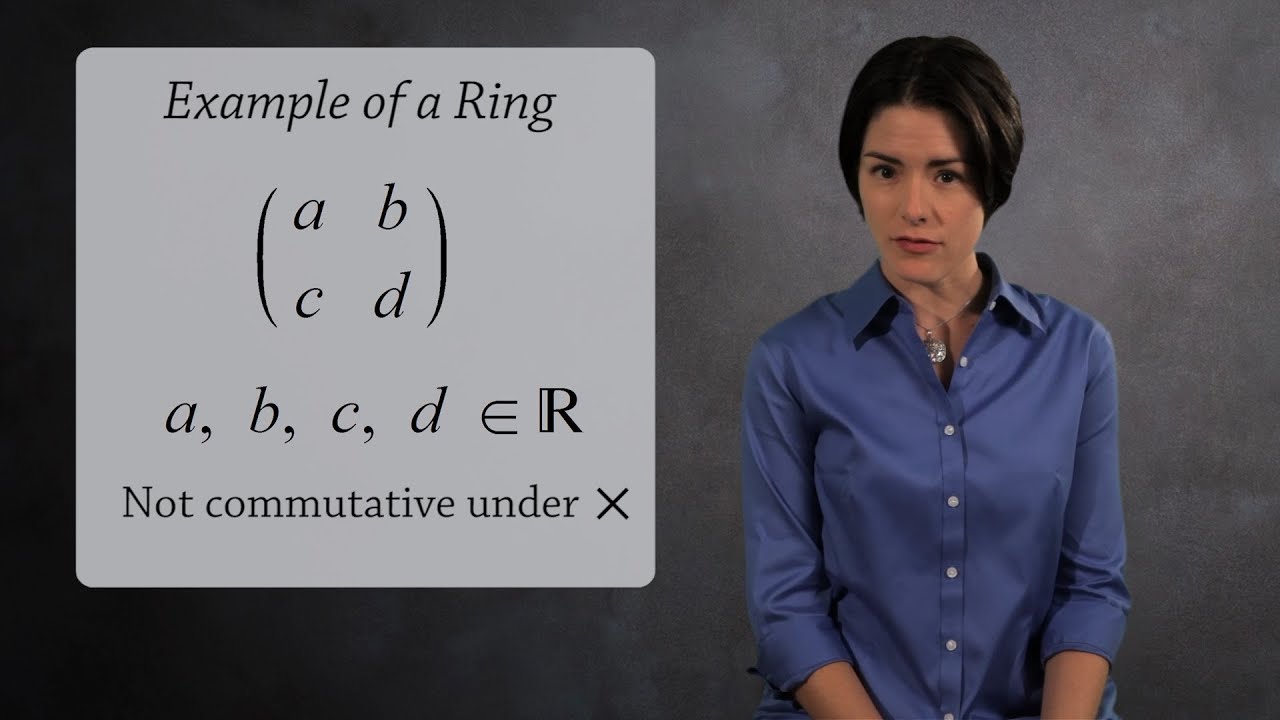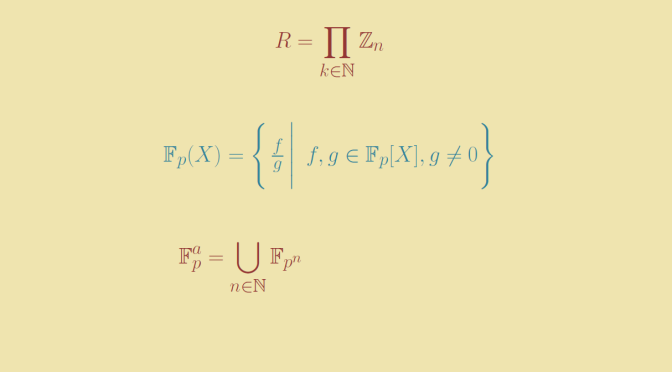Abstract Algebra Rings And Fields
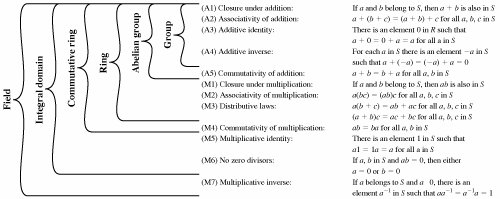
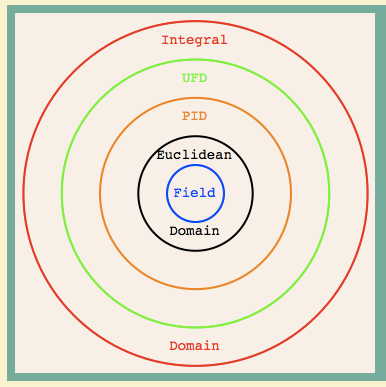
The most important are commutative rings with identityand fields.
Abstract algebra rings and fields. The term abstract algebra was coined in the early 20th century to distinguish this area of study from the other parts of algebra. A free module over r of infinite dimension. Different algebraic systems are used in linear algebra. A set of elements together with an operation performed on pairs of these elements such that.
Any algebra over a field. Commutative rings and fields. An introduction to groups rings and fields. Algebraic structures include groups rings fields modules vector spaces lattices and algebras.
The polynomial ring rx of polynomials over a ring r is itself a ring. A group is defined as. An algebra over a ring is itself a ring. Algebraic structures with their associated homomorphisms form mathematical categories.
A ringis a set r with two binary operations additiondenoted and multiplicationdenoted. The rational real and complex numbers are commutative rings of a type called fields. The operation when given two elements of the set as arguments always returns an element of the set as its result. Groups rings and fields.
These are also modules.
Best Abstract Algebra Books For Beginners Sharpen Your Knowledge
Solved Excercise C Parts 1 2 And 3 A Book Of Abstract
Https Encrypted Tbn0 Gstatic Com Images Q Tbn 3aand9gcqivo2cpggzisblwiewoqcimzv2l 2issabcvi5o 3teg4ccbwx Usqp Cau
Course Number Title Math 371 355 371 Modern Algebra Ii Credits
All The Other Structures Division Rings And Integral Domains And
