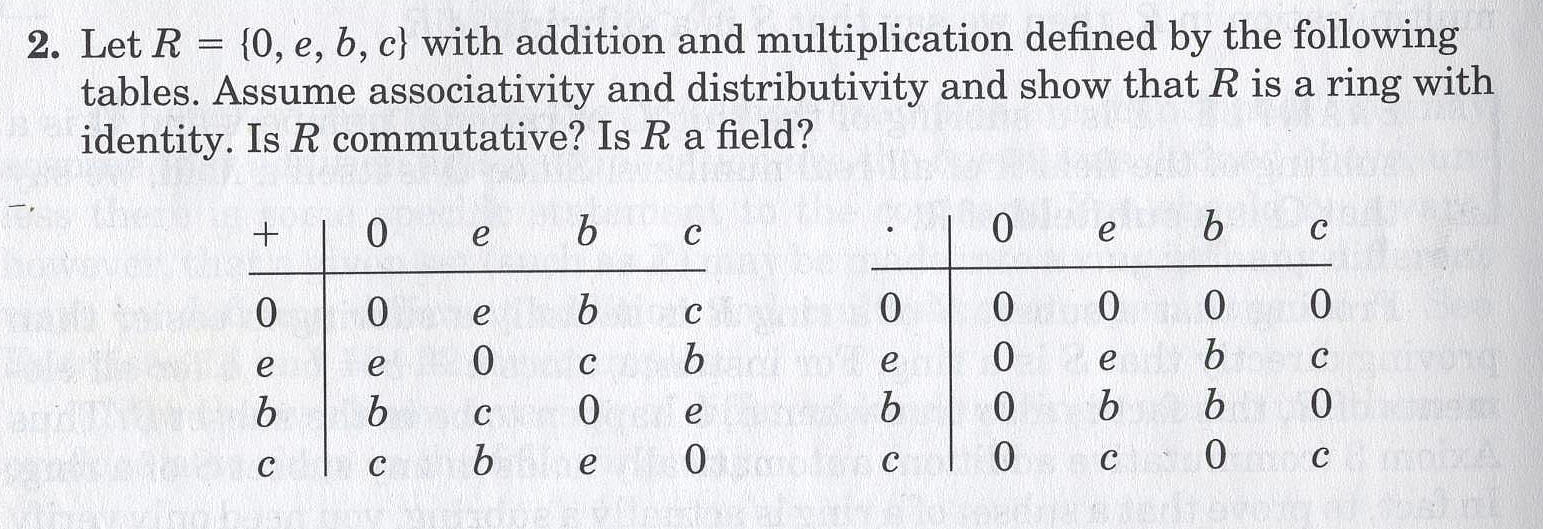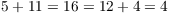Abstract Algebra Field Definition

Description abstract algebra deals with groups rings fields and modules.

Abstract algebra field definition. A field f is a triple that satisfies the following properties. The term abstract algebra was coined in the early 20th century to distinguish this area of study from the other parts of algebra. Category theory is a formalism that allows a unified way for expressing. F is an abelian group with identity denoted by 0.

We will first define a field. Algebraic structures with their associated homomorphisms form mathematical categories. In algebra which is a broad division of mathematics abstract algebra is the study of algebraic structures. A field is a non empty set with two binary operations and such that has commutative unitary ring structure and satisfy the following property.

They even appear in scientific topics such as quantum mechanics. In mathematics a field is a set on which addition subtraction multiplication and division are defined and behave as the corresponding operations on rational and real numbers do. The distributive law holds ie for all a b c f we have a b c a b a c. A field is thus a fundamental algebraic structure which is widely used in algebra number theory and many other areas of mathematics.