Abstract Algebra Basic Concepts

Chapter 1 of the text introduces the basic ideas from number theory that are a prerequisite to studying abstract algebra.

Abstract algebra basic concepts. Basic concepts elements in a ring. The ability to think abstractly is a valuable asset. Algebra is the language of modern mathematics. In these free videotaped lectures professor gross presents an array of algebraic concepts.

Lectures in abstract algebra vol. Pdf files can be viewed with the free program adobe acrobat reader. A right zero divisor is defined similarly. In algebra which is a broad division of mathematics abstract algebra is the study of algebraic structures.

Front preface and table of contents 110 k chapter 0 prerequisites 194 k chapter 1 group fundamentals 150 k chapter 2 ring fundamentals 222 k chapter 3 field fundamentals 135 k. For example in chapter 3 of the text you will be introduced to the concept of a group. This course introduces students to that language through a study of groups group actions vector spaces linear algebra and the theory of fields. A left zero divisor of a ring is a nonzero element in the ring such that there exists a nonzero element of such that.

The term abstract algebra was coined in the early 20th century to distinguish this area of study from the other parts of algebra. Many of the concepts introduced there can be abstracted to much more general situations. Basic concepts the university series in higher mathematics by nathan jacobson 1951 12 03 40 out of 5 stars 1 hardcover. Jacobson lectures in abstract algebra 2.

Abstract algebra helps develop this ability. Abstract algebra is an ideal capstone course for math ed majors and for those who will go on to grad school in math. Being able to do proofs in this setting is the main skill. The basic graduate year.

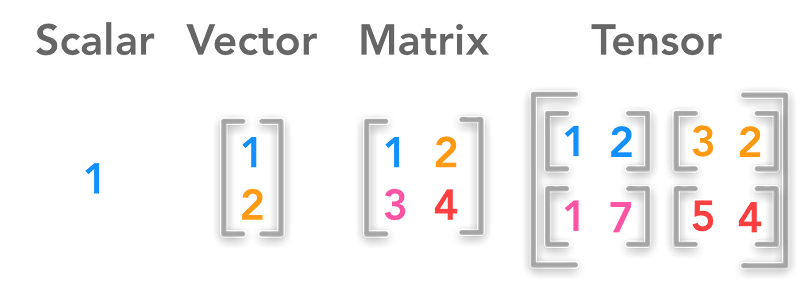
2 fundamental concepts of abstract mathematics. 2019 12 25 introduction to multiphase flow. Algebraic structures include groups rings fields modules vector spaces lattices and algebras. The central idea behind abstract algebra is to dene a larger class of objects sets with extra structure of which z and q are denitive members.

One of the rst broad. Many people are not comfortable with abstract concepts nor adept at abstract reasoning. Linear algebra graduate texts in mathematics 2009 06 06 n. 2010 04 11 lectures in abstract algebra 2.

Basic concepts applications and modelling zurich lectures on multiphase flow removed. Adding sets and quanti ers to this yields first order logic which is the language of modern mathematics. Category theory is a formalism that allows a unified way for expressing. Algebraic structures with their associated homomorphisms form mathematical categories.