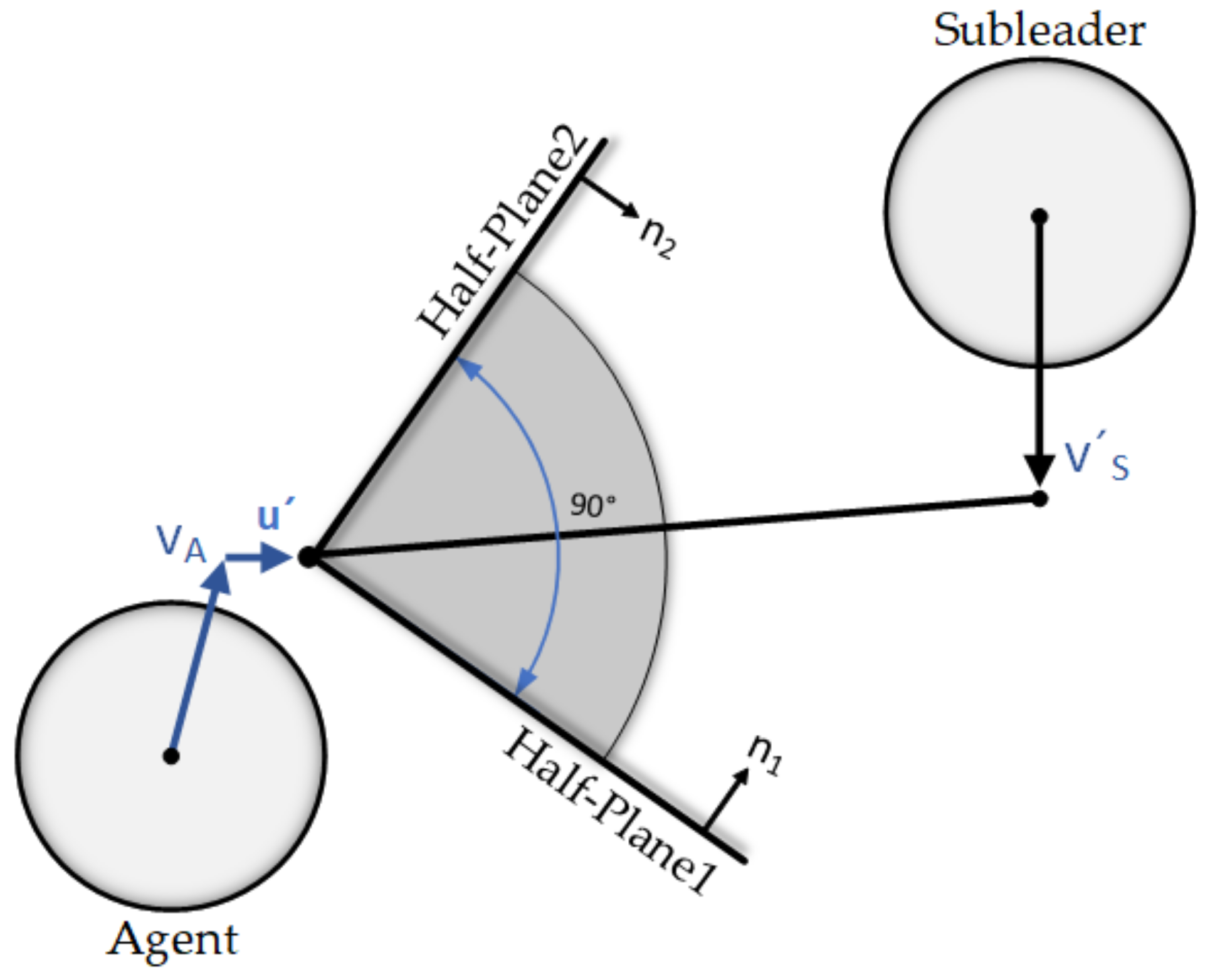
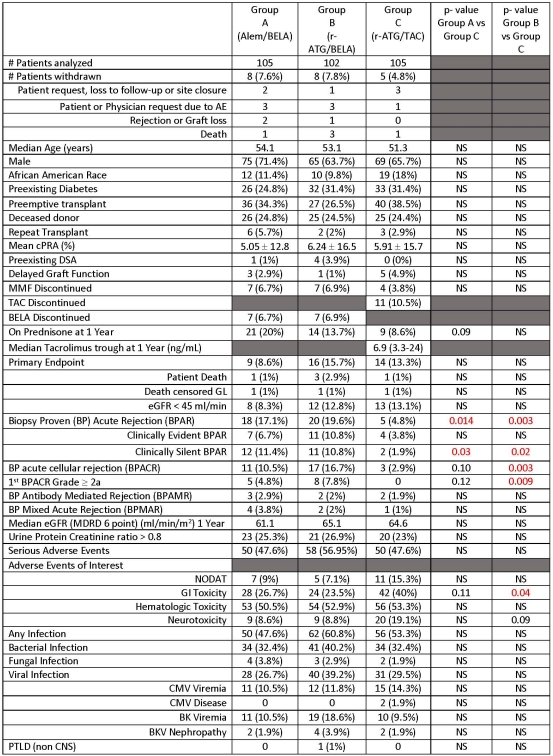
Abstract Group Vs Group

Other well known algebraic structures such as rings fields and vector spaces can all be seen as groups endowed with additional operations and axioms.

Abstract group vs group. Architect of record. 600000 sf terminal expansion. In mathematics and abstract algebra group theory studies the algebraic structures known as groups. The poincare conjecture proved in 2003 asserts that the fundamental group of a manifold which encodes information about connectedness can be used to determine whether a manifold is a sphere or not.

Before we begin to talk about abstract group discussion let us first understand what the word abstract actually means. The notation for the dihedral group differs in geometry and abstract algebrain geometry d n or dih n refers to the symmetries of. For instance algebraic topology uses algebraic objects to study topologies. Formal indeed all the above definitions of the word are reflected in most abstract group discussion topics.

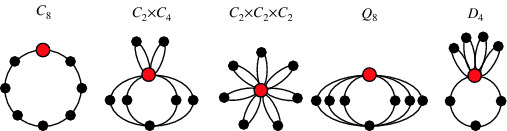
In mathematics a dihedral group is the group of symmetries of a regular polygon which includes rotations and reflectionsdihedral groups are among the simplest examples of finite groups and they play an important role in group theory geometry and chemistry. Groups recur throughout mathematics and the methods of group theory have influenced many parts of algebra. Let us first note that there were two meanings of the term abstract group during the first half of the 20 th century say from 1905 to 1955. This is a good reason why when considering z.

To explore groups mathematicians have devised various notions to break groups into smaller better understandable pieces such as subgroups quotient groups and simple groups. In addition to their abstract properties group theorists also study the different ways in which a group can be expressed concretely both from a point of view of. Linear algebraic groups and lie groups are two branches of group theory that have e. A place of work where designers can feel the joy of innovation be.

Of course multiplying as integers 2 3 6 and 6 is congruent to 1 mod 5. Cayleys theorem states that any abstract group is a subgroup of the permutations of some set x and so can be considered as the symmetry group of x with some extra structure. It is important to realise that the abstract definition of a group was merely an esoteric sideline of group theory through the 19 th century. In addition many abstract features of the group defined purely in terms of the group operation can be interpreted in terms of symmetries.

Abstract is an architecture firm that advocates a collaborative and interdisciplinary approach to design and explores the allied fields such as industrial and product design to draw inspiration and discover opportunities. This is not what is meant here by the abstract group r 1 r 2. Merriam webster dictionary defines the word as follows. And then takes the residue.

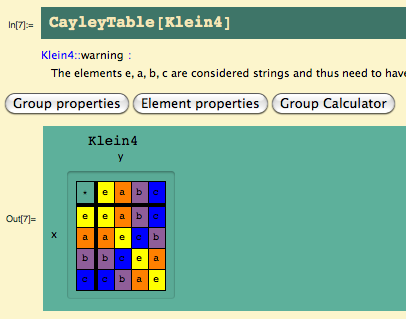
Our goal purpose is a firm that reflects the ethos captured by sony founder masaru ibuka when he said. One meaning was that of a group defined by the four axioms. For example in our abstract notation if we take n 5 then 2 3 0 in z 5 because 2 3 5 is congruent to 0 modulo 5. Disassociated from any specific instance difficult to understand.