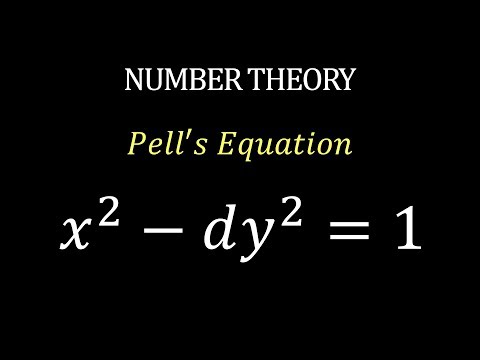Abstract For Pells Equation

The above technique may be generalized and used to show that any repeating simple continued. From our de nition of 1 k i0 1 in equation 4 we know that 1 k i0 1 1 so 1 k i0 1 1 p 5 2 as desired. Continued fractions and pells equation math 0420 introduction to number theory implies that 0 1 k i0 1 2 1 k i0 1 1 k i0 1 p 5 2.

The main result that is proven is the following.

Abstract for pells equation. If d is a perfect square then pells equation. In this article we formalize several basic theorems that correspond to pells equation. If x 2 n y 2 1 x2 ny21 x 2 n y 2 1 then the fraction x y frac xy y x is a good approximation for n. Solutions occur wherever the curve passes through a point whose x and y coordinates are both integers such as the trivial solution.

Pells equation alternatively called the p ell f ermat equation is a type of a diophantine equation of the form x2dy2 1 for a natural number d. The solutions to pells equation have long been of interest to mathematicians not least because of their value as approximations for n sqrtn n. We focus on two aspects. This article gives the basic theory of pells equation x 2 1 d y 2 where d is a parameter and x y are integer variables.

That the pells equation x 2 dy 2 1 has infinitely many solutions in positive integers for a given d not being a perfect square and that based on the least fundamental solution of the equation when we can simply calculate algebraically each remaining solution. Pells equation also called the pellfermat equation is any diophantine equation of the form where n is a given positive nonsquare integer and integer solutions are sought for x and yin cartesian coordinates the equation has the form of a hyperbola. If d is not a perfect square then there exists a fundamental solution x 0 y 0 that is not the trivial solution 1 0 and.