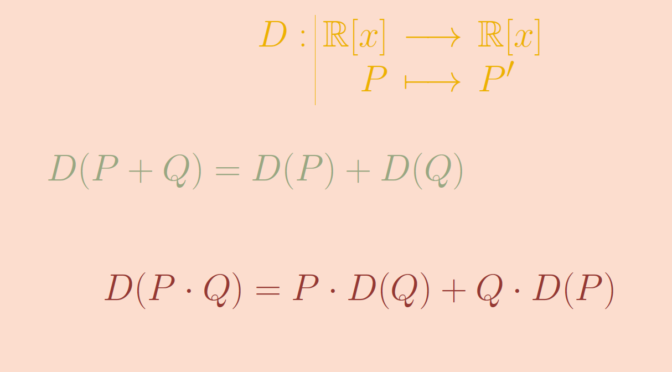Abstract Algebra Group Homomorphism

A fact about preimages under group homomorphisms. The kernel of a group homomorphism measures how far off it is from being one to one an injection. In algebra a homomorphism is a structure preserving map between two algebraic structures of the same type such as two groups two rings or two vector spaces.

It is a subgroup in g and it depends on f.

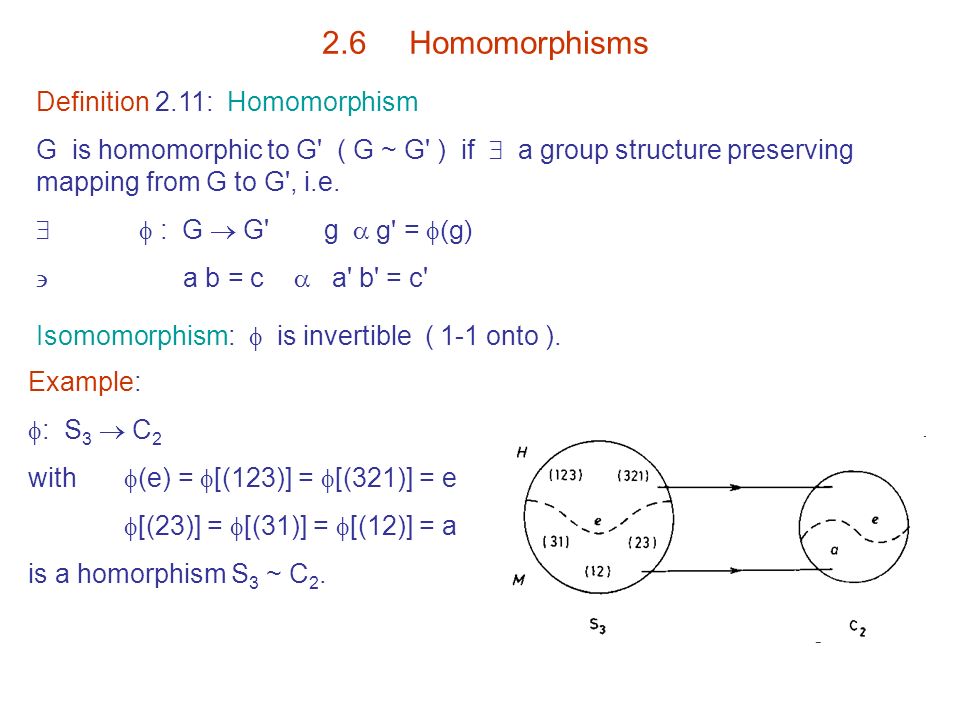
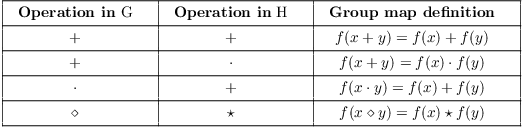
Abstract algebra group homomorphism. The coordinate projections from a direct product of groups are group homomorphisms. A homomorphism is called an isomorphism if it is bijective and its inverse is a homomorphism. Abstract algebragroup theoryhomomorphismimage of a homomorphism is a subgroup from wikibooks open books for an open world abstract algebra group theory homomorphism. Compute the center of a heisenberg group.

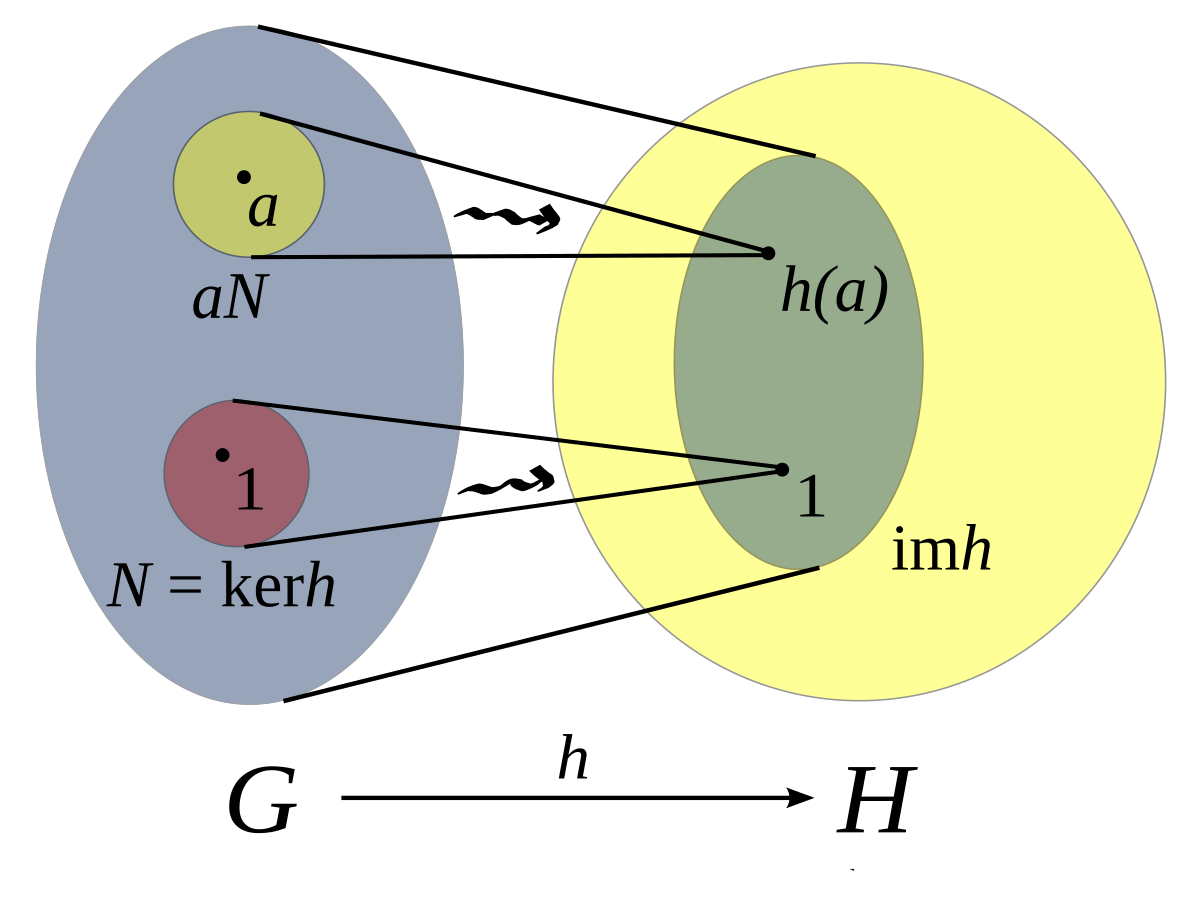
If a ring homomorphism as a map is injective then we say is injective. For example 11 2246 11 2. The word homomorphism comes from the ancient greek language. The kernel is the set of all elements in g which map to the identity element in h.

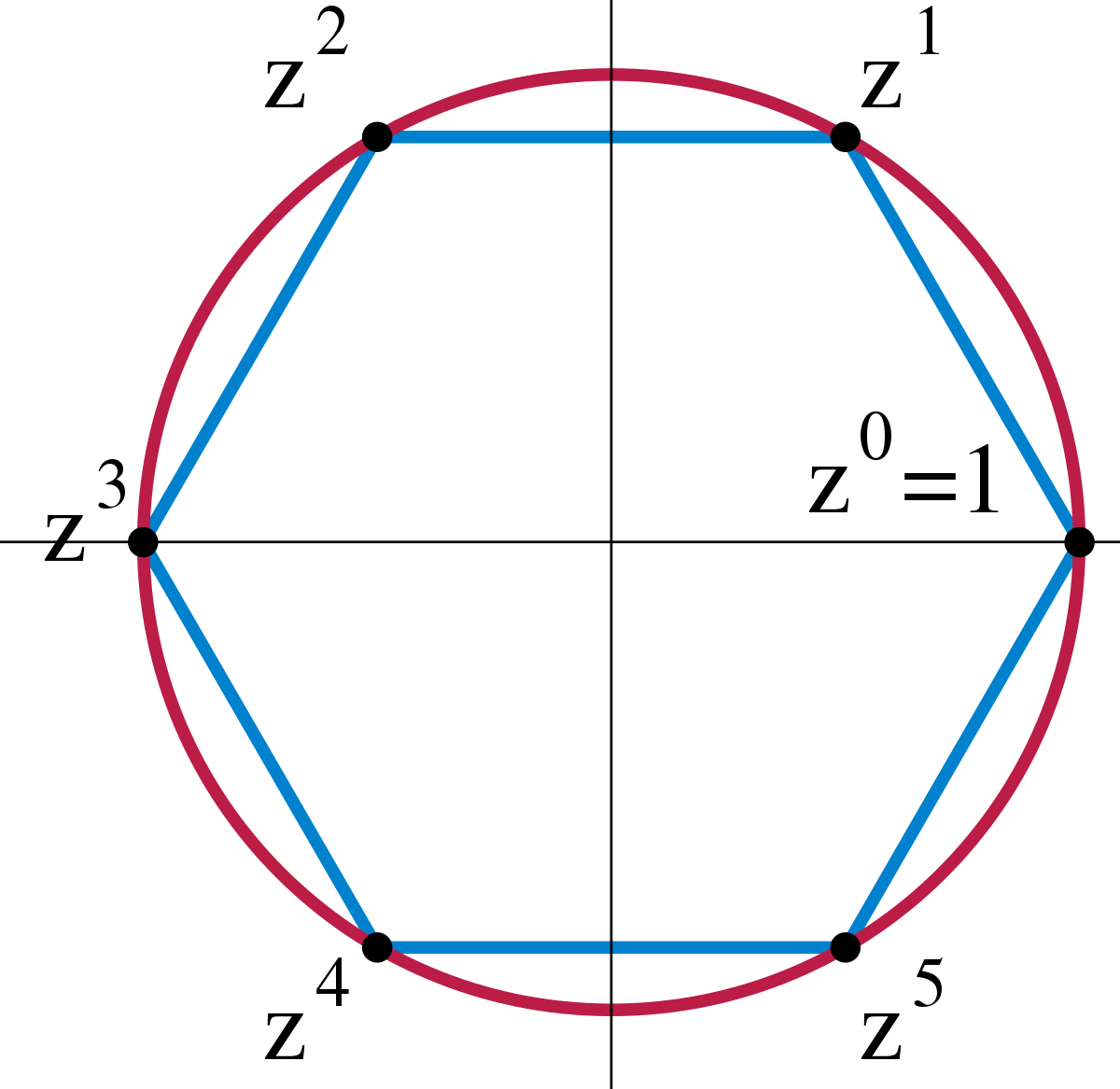
Omos homos meaning same and morfh morphe meaning form or shape. A group homomorphism is a function between two groups that identifies similarities between them. Qz is isomorphic to the group of complex roots of unity. Two groups are called isomorphic if there exists an isomorphism between them and we write g h displaystyle gapprox h to denote g displaystyle g is isomorphic to h displaystyle h.

Suppose you have a group homomorphism fg h. This essential tool in abstract algebra lets you find two groups which are identical but may not. Exhibit a group homomorphism from z8 to z4 describe the kernel and fibers of a given group homomorphism. Rings z and 2z.

Show that it is a group homomorphism actually a group isomorphism however it is not a ring homomorphism. Homomorphism group of homomorphisms between a homomorphism group and codomain of that group.