A Course In Abstract Analysis

A course in abstract analysis. The latter book intended for a year long course in functional analysis with measure theory assumed as a prerequisite is a considerably more sophisticated version of the second half of this book covering more material and at a higher level. A course in abstract analysis graduate studies in mathematics vol.

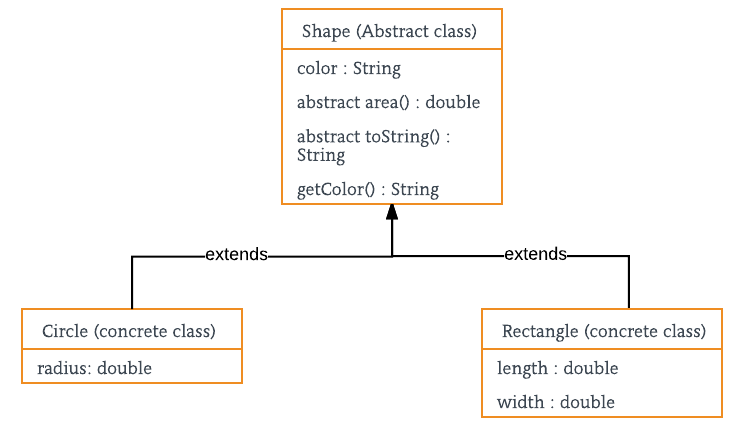
If a and bare algebras a homomorphism from a to b is a homomorphism such that x x for all x e a.

A course in abstract analysis. This book covers topics appropriate for afirst year graduate course preparing students for the doctoratedegree. Title htmla course in abstract analysis. The first half of the book presents the core of measure theory including an introduction to the fourier transform. These seven chapters invite comparison with the authors previous book a course in functional analysis.

A course in abstract harmonic analysis is an introduction to that part of analysis on locally compact groups that can be done with minimal assumptions on the nature of the group. Authors product displayjohn b. A b such that xy xy for all x yea. 2 a course in abstract harmonic analysis if a and b are banach algebras a banach algebra homomor phism from a to b is a bounded linear map.

141 qa312 conway mathematics george washington u presents a textbook for a year long course with a semester of measure theory followed by a semester of functional analysis to prepare first year. A course in abstract analysis. A course in abstract analysis john b. As a generalization of classical fourier analysis this abstract theory creates a foundation for a great deal of modern analysis and it contains a number of elegant results and techniques that are of interest in their own right.

Qa312c5785 2012 515dc23 2012020947 copying and reprinting. Volume 141 includes bibliographical references and index. Graduate studies in mathematics. A course in abstract harmonic analysis is an introduction to that part of analysis on locally compact groups that can be done with minimal assumptions on the nature of the group.

Affiliations htmlgeorge washington university washington dc. American mathematical society 2012 367 pages 7500 hardcover graduate studies in mathematics. A course in abstract harmonic analysis offers a concise readable introduction to fourier analysis on groups and unitary representation theory. This book covers topics appropriate for a first year graduate course preparing students for the doctorate degree.